How far away is the next 7-Eleven in Bangkok?
A Monte Carlo (MC) Simulation
Published: 14. September 2025

A 7-Eleven store in Bangkok with a monk.
Image from Felix Schickel
TLDR;
I spent 100$ on Google API calls to obtain a list with all 7-Eleven stores in the touristic center of Bangkok.
By further sampling 2e7 points and computing the distance to the respective closest 7-Eleven,
the average minimum distance to a 7-Eleven in Bangkok is around 193.5m!
Project is on github.
They are everywhere!
Just waiting across the street to fulfill your desire for a cold drink or offering you a snack.
The Japanese convenient store chain, 7-Eleven has over 15.000 stores in Thailand.
Especially in Bangkok you can find them at almost every corner.
But how many of them are there really?
Is the next one really around the corner or how far do you need to go?
I used the leftover credits of my google student account to answer those questions with the Google Maps APIs.
The plan was two-folded:
Firstly, retrieve all 7-Eleven stores in Bangkok using the Google Maps APIs and
Secondly, randomly sample a large number of locations in Bangkok and compute the distance to the closest store.
This will get the average shortest distance to a 7-Eleven store.
Getting all 7-Eleven stores in Bangkok
First, I needed a definition for the Bangkok city area. There are official polygon shapes of Bangkok as provided for example here by Open Data Bangkok. However, the actual area would be way too large for my computational resources, so I concentrated on the more touristically center of Bangkok. I created a rectangular polygon of the inner part of Bangkok. Visualized in Geopandas it looks like the following:
Polygon over the city center of Bangkok
This was the playground for the project. All points that were sampled were drawn from this shape.
After setting the perimeter, it was about to find all 7-Eleven stores in that area.
I scrolled through the Google Maps API documentation, seeking a suitable solution to find all of them.
The Routes API and the Places API with Text Search weren’t particularly helpful
as they either doesn’t allow for key word search or doesn’t accept coordinates
as the reference point from where to look for stores.
I ended up using the Nearby API which offers categoric search.
7-Eleven stores are categorized as convenience stores which is also a valid search category.
The approach from there is simple, I uniformly sampled 10k points from the Bangkok polygon
and sent a request for each of them to the Nearby Places API
to get a list with the closest convenience stores in a radius of 1km.
These 10k API calls costed me around 100$ of credits. A pretty lot for just finding all stores in Bangkok.
I would really like to know if there is just an easy way of browsing the Google Maps database in a SQL-like manner.
From the 10k sampled points, there are 1323 unique results. 988 stores of them have the term “7-Eleven” in their display name.
So, in this somehow arbitrary, more touristically defined area of Bangkok there are approximately 988 7-Eleven stores!
However, there is an uncertainty that this approach doesn’t capture all 7-Elevens present in that area.
There are two limitations to this approach: 1. The number of sample points may be too small to sufficiently cover the area and 2.
The API limits the response to a maximum of 20 stores around the sample point.
So, there might be under-sampled areas with stores not captured.
Therefore, 988 stores are only the lower-bound to the actual stores present.
Visualized on the map, each red dot represents a 7-Eleven store. There are also areas, less dense crowded,
where you can spot only a few stores. These are perhaps such under-sampled areas.
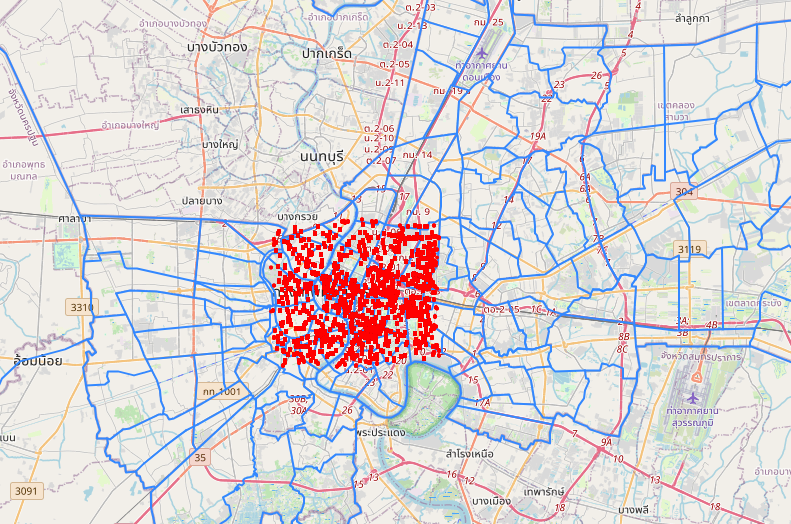
7-Eleven stores marked as red dots in the city center of Bangkok
Computing the distance to the next 7-Eleven store
For answering how far away the next 7-Eleven store is on average, I used a Monte Carlo based approach:
By sampling 20 million points uniformly at random from the shape, I computed the distance to the closest store for each of them.
With this approach you can estimate the overall average distance to the closest store.
Before computing the distances, the question of how to actually compute distances on a sphere arises to me as I never had work
work with geo data before.
Distances on a sphere
The most common distance metrics in Euclidean space are the L1 or L2 distance.
But as the points in this project are expressed in geo coordinates which are placed on a sphere and not in a Euclidean space,
the standard distance metrics are not applicable. I could have used the very practical Routes API to let Google figure out the walking distance
but as the approach is MC based, and I needed a lot of sample points I couldn’t afford to spend more on API credits.
So, I made the compromise between accuracy and affordability and decided to use the Haversine formula
which allows for lightweight calculation of the great circle distance. This is like the L2 metric in Euclidean space,
the straight line between two points, but on a sphere.
In a first attempt of the monte carlo estimation of the mean average distance to the next 7-Eleven,
I calculated for each sample point the distance to all 7-Eleven stores in the database
and then selected the minimum distance. This was the distance to the closest store.
However, to find the closest store to a given point, calculating the distance to every store in the database in a brute-forced like way
was somehow suboptimal. To optimize the retrieval, I used a KDTree.
It is a binary tree that allows an optimized k-nearest neighbor lookup. In this case, the number of neighbors was only one,
as I was only interested in the closest store. This approach allowed me to sample and compute 2e7 points with my hardware.
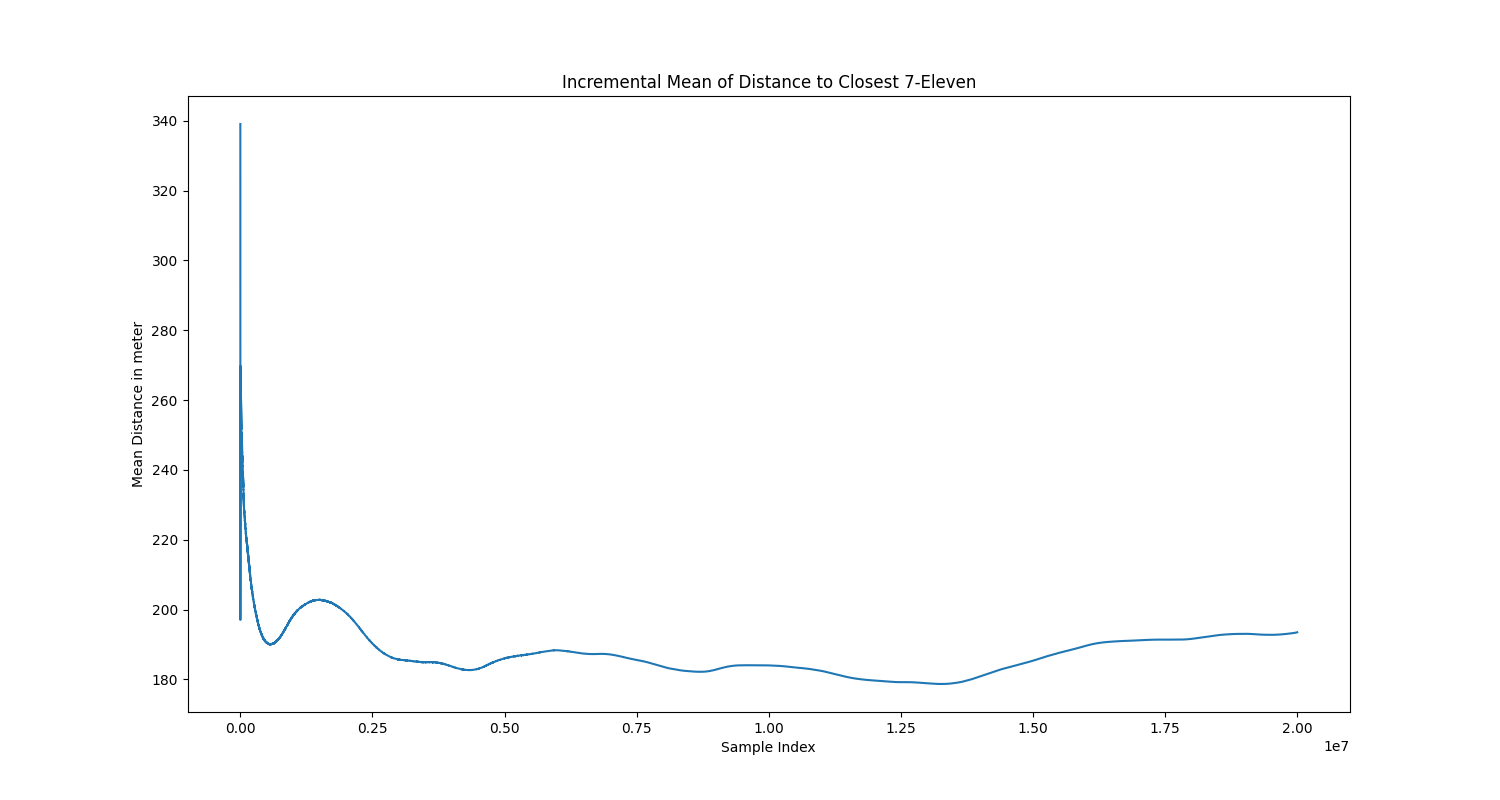
With each new point I computed the incremental average and plotted it below.
As there is no convergence criteria measured, I can give no statement about the convergence of the series yet.
However, after 20 million sample points, the average great circle distance to the closest 7-Eleven is 193.5m!
That’s around 1,5 minutes of walking. As the distance is measured as a straight line,
the walking distances will likely be a bit higher.
Summing up, the enormous density of 7-Eleven stores in Bangkok is astonishing.
With close to 1,000 stores in the center part you can get a snack within 2 minutes of walking on average.
I wish you good luck for finding your next 7-Eleven when in Bangkok! When you have the chance, give the Hot Chocolate Cake a try!
As this project was a short fun project for me, it was also really educational.
I learnt a lot about working with geo data and geopandas
There are also some shortcomings and limitations I explicitly want to point out:
- I used a somehow arbitrary definition of the Bangkok area. Mainly due to compute restraints on my side.
- The Google Maps Nearby API limits the search to 20 results per request. With the current approach, there might be some stores which are not retrieved due to a less dense spatial sample point distribution.
- The distance calculation between two points is a straight-line measurement with the Haversine formula. This is nothing more then a mere approximation of the walking distance in the real world.
- The Monte Carlo simulation was limited to 2e7 sample points, there are no real convergence criteria measured and with increased sample size there might be a different average.
Thank you for reading my first article!
If you have any feedback, I'd love to read it!
Send me a mail!
External link and mail icon by Icons8